They’re important. Kids who don’t know them will struggle later in math.
But many kids resist learning these facts, complaining that they are boring and pointless. And many parents dread them, having had similar experiences as students themselves (and maybe having forgotten their math facts by the time their kids are learning them).
Let’s look at how we can apply a bit of insight from learning science to make the times tables easier to learn and remember.
What’s the problem?
The multiplication facts are usually presented in a table like the one below (the familiar “times table”). We’ll focus on the facts from 1x1 through 10x10 here.The most common strategy for learning the facts is “brute force memorization” – which means using a combination of worksheets, drills, flashcards and the like to badger the brain into remembering this information through sheer repetition – that is, repeating the same problems over and over again.
If the brain were like the hard drive on your computer, this might be fine. In fact, we can enter the table of numbers above into a spreadsheet and save it to our computer’s hard disk on the first try – no problem at all.
But we know from brain research that your brain is nothing like the hard drive on your computer. In fact, brute force memorization alone is probably one of the worst possible ways for a human being to learn something. Brute force memorization can be unpleasant - no wonder kids resist it! – and it’s ineffective. Even if you manage to hammer the information in there, it’s more likely than not to leak away pretty quickly.
There is a better way
The brain isn’t set up to store large numbers of isolated facts rapidly (like a hard drive). Instead, it’s set up to identify and encode meaningful patterns.What kinds of patterns? Well, visual relationships and symmetry are two good examples. Let’s take a look.
How is the times table constructed?
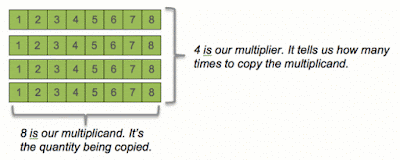
Have you ever thought about where the times table comes from? To understand that, first think about what a multiplication represents.If we take a multiplication like 8x4, we are saying we want to copy one number (the multiplicand) a certain number of times (the multiplier). There’s no hard and fast rule about which order the multiplier and multiplicand are written. For our purposes, consider the first number (8) to be the multiplicand (the number being copied) and the second number (4) to be the multiplier (the number of copies). So in this case “eight times four” means “copy the number eight, four times.” (Note that the word “multi-ply” is derived from the words for “many layers” – you can see why in the diagram below).
How do we get from the four eights to the result of the multiplication (which is 32)? Easy – just count out the number of squares in the whole rectangle like so…
The familiar times table is made up of all the rectangles representing all the multiplications from 1x1 to 10x10 laid one on top of the other, so that only the very last square of each one - containing the final count of squares in that rectangle - peeks through. If you look at the cell for the multiplication of interest, you can see that it is at the top, right corner of a rectangle that represents the multiplication of interest (and covers that number of squares).
This visual relationship between the individual multiplication problems and the structure of the whole table can help students understand and remember the facts, because they can start to picture the problems visually in their mind’s eye. Also, if they forget one of the facts, then this conceptual understanding gives them a way to reconstruct it from known facts nearby.
How can symmetry help students learn the facts?
Consider the multiplication 8x4=32. This means, “copying eight squares four times gives you thirty-two squares.” Notice that 4x8=32 means something different, namely “copying four squares eight times gives you thirty-two squares.” The picture below shows the two visually.The rectangles represented by the two multiplications are different shapes, but they give the same result in the end (32 squares). This works for any two numbers you multiply – changing the order changes the rectangle’s shape but doesn’t change the quantity that results. This is called the commutative property of multiplication.
Now let’s apply this insight back to our times table. Look at the table below. It’s the same as the one above, but color-coded to highlight the symmetry associated with the commutative property. Notice that if you folded the table on its diagonal, the numbers in the two halves would overlap perfectly.
For students, this is great news – it means instead of memorizing all 100 facts, they can learn 55 facts (45 facts in one of the triangles plus the ten facts along the diagonal that are perfect squares like 1x1 or 4x4 – on the diagonal the multiplicand and multiplier are the same and so they have no mirror image). Learning this one relationship cuts the number of facts almost in half instantly.
Multiplying by 1: Mono-plying
We can cut the number of facts down further by looking at specific groups of facts. Multiplying by one, for example, is not really multiplying at all – it’s mono-plying (if multi-ply means “many layers” then mono-ply means “one layer”).Remembering the mono-plying rule (multiplying any number by 1 gives you back that same number) takes care of another ten facts, leaving us with just 45 facts to learn.
Multiplying by 10
Multiplying tens is easy, too. It’s just like multiplying by one except you append a zero to the result.2x1 = 2 and 2x10 = 20 = “twenty” (derived from the words “twin tens”)
3x1 = 3 and 3x10 = 30 = “thirty” (derived from the words “three tens”)
4x1 = 4 and 4x10 = 40 = “forty” (derived from the words “four tens”)
and so on…
To see why, look at the picture.
Adding the rule for multiplying tens takes care of another nine facts, leaving just 36 to learn.
If 36 multiplication facts still seems like a lot, consider that there are 26 letters in the English alphabet plus ten digits that have names (zero, one, two, etc.), which is also 36 facts. Your child memorized those, and you can use the same kinds of techniques for the remaining 36 times table facts. Just keep in mind that helping a child to understand where the facts come from along with patterns like the visual relationships between rectangles and the symmetry that comes from the commutative property will make learning the facts (and other things later, like long multiplication, division, and algebra) much easier. The knowledge will also stick better and last longer.
Summary
To summarize, we started with 100 multiplication facts to learn, from 1x1 through 10x10.First we introduced a few key concepts:
- What is multiplication? It’s copying one number a specified number of times (as in “eight times four” and “times table”) and counting up the quantity that results
- Where does the times table come from? From stacking all the multiplication rectangles on top of one another, letting just the last square of each with the total quantity for that rectangle show through
Then we introduced a few key rules:
- Commutative Property: It doesn’t matter which order you multiply two numbers – it means something different but you still get the same result (Example: 8x4 = 4x8 = 32)
- Multiplying by one (or mono-plying): When you multiply any number by one, you just get that number back
- Multiplying tens: Just like multiplying by one, except you append a zero to the result (Example: 1x4 = 4 and 10x4 = 40). Remember: the name “forty” is just a short form of “four tens”
With these few rules we cut down the number of facts to a manageable 36. Not only does this reduce the memorization load by about two-thirds, but the conceptual understanding will make the remaining facts easier for students to learn and remember.
Additional resources
This is a lot of information (who knew there was so much to know about the lowly times tables?).Some teachers, tutors, and parents can make use of it in the form it’s presented here in the blog post. To make it easier for everyone else, I’ve packaged this information up into some free videos and a couple of inexpensive apps for iPhone and iPad - each priced less than a pack of index cards. (Note: If you are searching for one of the apps on an iPad, you'll need to change the default filter from "iPad" to "iPhone" apps to find them).
Another great way to help kids learn is to insert yourself into the process – show them you’re interested and available to help if they need it. The same way you read books to your children when they were small, you can sit with them and work through some math mini-lessons at the table, in Minecraft, or using these apps.
Video examples of using Minecraft to learn arithmetic:
- Minecraft Math #1: Numbers - Even, Odd, Prime & Square Root
- Minecraft Math #2: Addition, Multiplication & Commutativity
Bognor’s curse – An Interactive Educational Mini-Adventure
Something’s gone terribly wrong at the Ministry of Magic. The evil wizard Bognor has cast a terrible curse across the land and it’s up to you – a lowly apprentice – to defend your village and defeat his dark magic. To succeed, you’ll have to master some basic Arithmancy. Will you do it?
Watch the video
Experience the magic
Something’s gone terribly wrong at the Ministry of Magic. The evil wizard Bognor has cast a terrible curse across the land and it’s up to you – a lowly apprentice – to defend your village and defeat his dark magic. To succeed, you’ll have to master some basic Arithmancy. Will you do it?
Watch the video
Experience the magic
Multiplication Explained – Master the Times Tables with Understanding
Multiplication Explained is more than a typical flashcard app. It is a complete mini-curriculum designed to promote both conceptual understanding and fact fluency at the same time.
Watch the Video
Get the App
Multiplication Explained is more than a typical flashcard app. It is a complete mini-curriculum designed to promote both conceptual understanding and fact fluency at the same time.
Watch the Video
Get the App
Comment and share!
I always love to hear from parents, teachers, and students about ways I can make these resources more useful to help you learn and teach, and what other topics you would like to explore in the blog.












So…Minecraft for education. I’ve been thinking a lot about this. I AM convinced of its value in education for open-ended creative play, critical thinking, problem solving, research skills, etc., etc. Your two activities provide excellent models of this. I think a missing piece, for education overall, is the meta-cognitive process of reflecting on “what did I learn.” But, I’m going to take a bit of a turn on this question (the value of Minecraft and building excellent learning opportunities in content areas) to something one off.
ReplyDeleteThe linked article (below) intrigues me—because I am the parent of a young adult on the spectrum, and a former teacher. I’d love to hear from “experts” in this field: parents, teachers, speech pathologists, psychologists, cognitive neuroscientists, music therapists, game designers…and those amazing individuals on the spectrum! What is needed to effectively use Minecraft for education in content areas AND in social skill building? How can we do this with intentionality and how can we measure any growth and transfer of all these skills? Any parent of a child who is “obsessed” with the gaming environment must know that these kids ARE involved in social networking and interaction; but how do we ensure this transfers “off-line” in face-to-face interactions?
From http://tinyurl.com/psbnpfa
Louden says these “communities of practice” are also springing up spontaneously among parents and specialists who work with ASD children as they search for ways to adapt the game to the needs of those with autism.
“Anything that boosts the confidence of these kids, that allows them to be the experts, the masters of their own environment, is a path that we should explore,” said Louden. “The “gamification” of these life skills is bringing about a new class of interaction between those with autism and the neurotypical world. It’s a bridge we need to continue to build.”
Rene,
DeleteHave you looked at Autcraft? (http://www.autcraft.com/)
It's a Minecraft server for children and adults with autism and their families (mentioned in the article you linked).
Also, examples of impact Minecraft can have on children on the spectrum:
http://www.buzzfeed.com/charliewarzel/this-minecraft-community-is-saving-the-lives-of-children-wit#.kyaz5MyDj
Thank you for this link! Great, moving article! Yes, I had looked up Autcraft when I found the link I mentioned. Stuart Duncan, this amazing father, is now on my wall of heroes; and I only have a few heroes on that wall.
DeleteTaking a sharp left turn away from my specific discussion about social skills training/transfer, back to a takeaway point of your post, here's what I think you were getting at: How can we use technology to teach to understanding/mastery, without frustrating a student to tears! Lots of tears! And probably some screaming, pencil breaking, tearing paper, name calling, blaming…we’ve all seen it, or lived it. All that can lead to math anxiety. Math anxiety is R.E.A.L. Test anxiety is real. (Those two are worthy of their own blogs.) What I think you’ve hit on, and maybe you didn’t mean to address this aspect, is that with technology we really do have the opportunity to use a different resource to teach; one without negative social feedback (even unintentional) from humans ---That is IF it has been explicitly and intentionally embedded in the design.
The bigger questions, for me, and ones I throw out to your readers, are:
1) As a teacher (or parent/administrator/developer/funder/other stakeholder), am I looking deeply at the technology students need?...the technology they are using? What am I measuring?
2) Looking at the sheer number of text books AND how FEW have actually been researched for evidence of effectiveness, will I take this “do-over” chance and demand this with technology? How?
3) What am I doing personally, besides talking, about integrating/using/evaluating technology in education? What do I need to move from talking to action? What can I do, reasonably?
4) Last, what can I glean from observing the Autcraft members , those with ASD who struggle, sometimes in emotionally painful ways, with social interaction, as they learn, build, and collaborate to problem solve for the “greater good?” (That's a trick question, BTW)
What I appreciate about Stuart Duncan, is that he (in my mind) asked himself similar questions and he did something about it…and it has had an impact on thousands!!! People like you write blogs, create software, ask questions, because you really do want to illicit positive change; and you’re doing something about it. All of this is risky and sometimes scary. Frankly, I think Stuart’s virtual learning community proves it was worth the risk. (Easy for me to say!) What can we, your readers, do to help identify and remove risks in order to support you, and others, who are trying to teach (multiplication facts/anything else) without tears? --Readers, that's a trick question, too, read Mike's "Comment and Share!" section for a small start. :-)
This comment has been removed by a blog administrator.
ReplyDeleteAnother wonderful contribution to the conversation and one that brings up the opportunity to point out an opportunity for teachers in class to leverage the brain's ability to detect patterns. Teachers often feel compelled to name the patterns that they or the field has already identified. For example you note: in the section of symmetry, “This [regarding rectangles of equal sums] works for any two numbers you multiply – changing the order changes the rectangle’s shape but doesn’t change the quantity that results. This is called the commutative property of multiplication.” As a teacher I would invite other teachers to resist naming this pattern for students, and, instead invite them to consider first whether this observation really is a pattern across the table, and, secondly, whether it is worth naming. If students accept this challenge of naming the rectangles of equal opportunity (that's my name), then see what name they invent. You can build on this moment by then inviting them to consider the name that the field has already given this pattern, and to consider the differences (or similarities) in names.
ReplyDeleteThe second pedagogical opportunity builds on work of pattern recognition, by asking students if they can find symmetry in the table. They might not know what symmetry means but discovering the meaning of symmetry can be an activity in of itself. Using a mirror is one way to discover the meaning of symmetry, and then the concept can be applied to the table. I would be interested in seeing what students discover before revealing the diagonal, and, I predict, so will they.
Marc,
DeleteThank you for sharing these great ideas for how to actually teach this in a classroom.
Your suggestions also provide excellent concrete examples of a powerful, general educational principle.
The brain has different types of memory systems, and the "same" information (e.g., the times tables) can be organized in very different ways in the child's nervous system. Some organizations are much, much better than others.
The people who create knowledge - the ancients who discovered (invented?) zero, developed our Arabic numerals, worked out our system of place value and arithmetic operations like addition and multiplication, for example - go through a constructive process where each piece of information fits coherently into a larger hierarchy of knowledge. They understood the meaning of numbers, the reasons for the quirks of our place value system, the relationships between addition and multiplication, the structure of the times table, the importance of commutativity, because they had to construct each piece of knowledge by building on top of existing knowledge. They could use that knowledge effectively because they understood not just the facts but the reasons for those facts and the relationships between them.
What we do in textbooks is skim the top layer of information - the facts and figures, rules and algorithms - and try to get kids to memorize it all as a list of decontextualized, disconnected facts. It seems more efficient - why make them go through the steps of getting to these ends when we can just give them the ends directly?
One reason is because this efficiency notion is actually just plain wrong when we consider how the brain learns. Imagine you had to learn a story like "Goldilocks and the Three Bears." Most of us could relate it by heart on the spot and the rest of us could recognize what story it was without being told the title. Now imagine you had to memorize a list of phrases pulled from a printed version of the same story, in no particular order, with each phrase being given a number to identify it, such that if the teacher called out the number you had to recall the phrase exactly. We would do pretty poorly on that, especially decades after studying it.
Isn't that the "same" information in two forms similar to how the times tables is the "same" information if we just have kids memorize the facts and laws vs. understanding how the parts relate?
The brain doesn't do well with memorizing disparate facts - it's a very inefficient way to learn something. It does well with patterns and relationships - temporal ordering and cause-effect relationships in the story, for example, provide a lot of information that helps us remember it for decades.
As Piaget, the great developmental psychologist, put it:
"Each time one prematurely teaches a child something he could have discovered himself, that child is kept from inventing it and consequently from understanding it completely.”
kids learning numbers
ReplyDeleteIf take a look at our education system, the amount of outdoor time children are allotted gradually declines overtime as they progress through their education. arabic language course hong kong
ReplyDeleteThis information is impressive; I am inspired with your post writing style & how continuously you describe this topic. After reading your post, thanks for taking the time to discuss this, I feel happy about it and I love learning more about this topic..
ReplyDeleteHuman Resource Assignment Help
waoo well written post regarding "Learning the Times Tables? Here's How to Do It - Without Tears!"
ReplyDeleteThanks,
Intraday Trading Tips On Mobile
Pretty article! I found some useful information in your blog, it was awesome to read, thanks for sharing this great content to my vision, keep sharing..
ReplyDeleteDirect Admission In VIT University Through Management Quota
Direct Admission In VIT University Under Management Quota
VIT University Direct Admission
Please try my multiplication tables speed test:
ReplyDeletehttp://Aztekium.pl/Master
http://Aztekium.pl/Multiplication
This comment has been removed by the author.
ReplyDeleteKids Education
ReplyDeleteKids Educational Channel
Kids Educational Videos Channel
ReplyDeleteWe believe in the motto ”learn and develop while playing”.Your tiny tots get the learning experience with creative and playway of coaching. Located in Chennai we are the best school in Perambur and Best school in Vyasarpadi. It is always good to read some great article like this, thank you so much for the post. Please do help me suggest
The Best School in Perambur
The Best School in Vyasarpadi
thank you for sharing this useful article regarding education.mitjuniorcollege offers cbse pattern education in Arts ,commerce and scienceClick here
ReplyDeleteHaving the scored in India discharges that fabricate from captains likewise arranges it in the crisiss of lecturers who drive altogether inquiry American idioms or cultural materials. Mbbs in Xian Jiotong University
ReplyDeleteThanks sir for sharing your thoughts with us. Truly this is nice information and useful. Our expert provide essay writing and Term Paper Writing Services.
ReplyDeleteThis is really a very good article. Thanks for taking the time to discuss with us, I feel happy about learning this topic. keep sharing your information regularly for my future reference.
ReplyDeleteIB School UAE
Very good post.
ReplyDeleteAll the ways that you suggested for find a new post was very good.
thesis writing
Best digital marketing institute in delhi
ReplyDeleteBest digital marketing course in delhi
Digital marketing institute in delhi
Digital marketing course in delhi
call us: 9212265265
Nice Article!
ReplyDeleteBook Hire Car, Taxi, limousine or chauffeur car for your transportation trip now online from the website or call on 0390882016
Melbourne Silver Service
Melbourne Silver Taxi
Silver Top Taxi Melbourne
Silver Taxi Melbourne Airport
Melbourne Silver Airport Taxi
Silver Taxi
Silver Melbourne Service
Official News has released by the the Rsmssb, Rajasthan Patwari Bharti 2019 Rajasthan , redarding the Rajasthan Patwari Recruitment 2019 patwar Vacancies in Rajasthan. We will provide Rajasthan Patwari Vacancy 2019 the method by which you can download the latest official Advertisement of Rajasthan Rajasthan Patwari Vacancy 2019 Rajasthan Patwari Bharti News 2019
ReplyDelete
ReplyDeleteThank you for posting such great article it helped me a lot.
regards:
Learn French Online
STEM toys UAE
ReplyDeleteBuy stem toys online for your kid's education at an affordable price in UAE. StemToysShop offer the best stem toys and science education toys for children in the UAE.
to get more - https://stemtoysshop.com/products/number-balance-math-toys
Fact Zone
ReplyDeleteHi People, The notifications for forest watcher declaration form has now been announced and you can see all here.
ReplyDeleteThis exam is just amazing and is a government job exam.
So prepare for it well and visit our website for any help.
Thanks.
Hey, I Just found your post by searching on Google, I am Impressed and Learned Lot of new thing from your post. I am new to blogging and always try to learn a new skill as I believe that blogging is a full-time job for learning new things day by day.
ReplyDeletebritish english speaking course in gurgaon
corporate training in gurgaon
spoken english classes in gurgaon
Great Post! I learned many new things about education. I am sure people will take all the advantage to help other people through education.
ReplyDeleteStem school
ReplyDeleteSTEM Education for kids explore programmes and resources that support overall development for your child. Resources Professional Development Bursaries STEM Education for Parents Discover projects, activities and challenges to engage young people of all ages with world and wonder of STEM subjects and careers. STEM Clubs.
to get more - https://stemtoysshop.com/pages/stem-school
Pigso Learning is the best exam app in Gujarat. It is available language Gujarati, Hindi, English. So you can download our app for exam preparation app.
ReplyDeletejudi poker idn online
ReplyDeleteidn poker terpercaya
poker88
Its full of information I am looking for and I love to post a comment that "The content of your post is awesome" Great
ReplyDeletewill help you more:
We offer online Expert Writing Help for Academic Writing Services at all levels. Don't get stuck with your papers. Let us assist you.
nursing essay writing service
I found some useful information in your blog, its very useful, Thanks for sharing this great content to my vision, keep sharing..
ReplyDeletemasters cap and gown
Hello my name is Mirai Yu.. i want tell a little about my hobby is Shopping, Photo Shooting and singging. and if u want know more about me, u can visit my Offocial Website :D
ReplyDeleteIDN Poker
This comment has been removed by the author.
ReplyDeleteHere you will find latest online sweepstakes, Contests and Giveaways and win lots of cash prizes or more.
ReplyDeletesweeptakesvalue.com
Essence Festival Ford Vehicle Sweepstakes
Green Bay Packers 12 Days of Summer Giveaways
APT 2B Staycation Bedroom Suite Sweepstakes
Food Network Magazine Color This Dish Contest
PrizeGrab $5,000 Cash Giveaway
Viably, the article is actually the best point on this library related issue. I fit in with your choices and will enthusiastically foresee your next updates.
ReplyDeletehrdf claimable training
Especially superb!!! Exactly when I search for this I found this webpage at the top of every single online diary in web crawler.
ReplyDelete360DigiTMG data analytics course
This is a great motivational article. In fact, I am happy with your good work. They publish very supportive data, really. Continue. Continue blogging. Hope you explore your next post
ReplyDelete360DigiTMG data science training
You finished certain solid focuses there. I did a pursuit regarding the matter and discovered almost all people will concur with your blog.
ReplyDeletehrdf training course
http://paddingforrecliner.blogolize.com/
ReplyDeletesofafordogs
bestkidschairsofa
kidscouchesandsofas
sofasforkids
I looked at some very important and to maintain the length of the strength you are looking for on your website
ReplyDeletedata science course noida
Super site! I am Loving it!! Will restore again, Im taking your food moreover, Thanks.
ReplyDeletecyber security course in malaysia
Thanks for this, This is exact I Am searching for In Google. Thanks for sharing.
ReplyDeletetinder pour pc
tindersurpc
tinder sur pc
tinder pour pc 2021
I really enjoyed reading this site, this is a great blog https://makerspace.aisingapore.org/community/profile/situs988poker/
ReplyDeletecashback melimpah? sudah pasti hanya di bandar togel online kingdomgrup http://128.199.187.54/
ReplyDeleteThis post is very simple to read and appreciate without leaving any details out. Great work!
ReplyDeletedata scientist training in malaysia
Hi ! welcome to my Website Here You can download free software And get Right Link you want And Free Registration keys Are
ReplyDeleteAvailable For Paid Software it is completely Secure And Free .I Hope You will Check It Out And Enjoy A lot.
please Click On the Link Provided .Up4Pc-
www.bluehost.com
ReplyDeleteSuperb Hosting service for your website amazing features free panels low price www.bluehost.com
ReplyDelete
ReplyDeletetransfer money easily anywhere in the world Your micro bank in you pocket join Payoneer affiliate
marketing and strat earningPayoneer
Lakukan perawatan motor anda di Bengkel Motor Bekasi dan Kunjungi Juga website kami http://www.bengkelmotorbekasi.com untuk mengetahui selengkapnya layanan kami
ReplyDeleteDo you want to earn more money easily, here is the link of link shortener just click and see and start earning you
ReplyDeletewill get bounus and more earn money-
I am impressed by the information that you have on this blog. It shows how well you understand this subject.
ReplyDeletefull stack development course
PPB SYLLABUS & STUDY MATERIAL:- As a banker, you must have heard about the JAIIB Exam that is basically conducted for the bankers and some of its benefits for passing the said Exam. Not only do you get the benefit of One Increment of 1 year in advance but also will be eligible to sit for the CAIIB afterward which again gets you 1 increment in advance.
ReplyDeleteIIBF JAIIB PPB STUDY MATERIAL 2022 EXAM
https://learningsessions.in/ppb-syllabus-study-material/
Very awesome!!! When I seek for this I found this website at the top of all blogs in search engine.
ReplyDeletefull stack development course
Excellent information on your blog, thank you for taking the time to share with us. canaan avalon 1246
ReplyDeleteThrough this post, I realize that your great information in playing with all the pieces was exceptionally useful. I advise this is the primary spot where I discover issues I've been scanning for. You have a smart yet alluring method of composing.
ReplyDeletePleasant data, important and incredible structure, as offer great stuff with smart thoughts and ideas, loads of extraordinary data and motivation, the two of which I need, because of offer such an accommodating data here.
ReplyDelete360DigiTMG, the top-rated organisation among the most prestigious industries around the world, is an educational destination for those looking to pursue their dreams around the globe. The company is changing careers of many people through constant improvement, 360DigiTMG provides an outstanding learning experience and distinguishes itself from the pack. 360DigiTMG is a prominent global presence by offering world-class training. Its main office is in India and subsidiaries across Malaysia, USA, East Asia, Australia, Uk, Netherlands, and the Middle East.
ReplyDeleteGreat! If you are looking for Allopathic Range Pharma Business in West Bengal
ReplyDeletethen you can contact us.
Awesome! If you are looking for Gynae PCD Franchise Company in West Bengal
ReplyDeletethen you can contact us.
Buy dog raincoat online at best price. All4pets offers you rain coat that are of good quality, light weight and comfortable all around the rainy season.
ReplyDeletebuy Dog Raincoat AT BEST RPICE ONLINE IN INDIA
Buy Protein Bars - Musclife healthy & delicious meal replacement snacks protein bars online in India at best prices with 6 different flavours available
ReplyDeletebuy Buy protein bars online india ONLINE IN INDIA
Chopping board is a kitchen material. It is usually used in chopping raw meat, dairy products, fruits, vegetables, nuts. The chopping board is depend on your need.
ReplyDeletebuy Plastic And Steel Chopping Boards ONLINE IN INDIA
10 Best Wooden Chopping Boards in India. By the way, there are many types of chopping cutting boards, which can be called marble, steel etc.
ReplyDeletebuy best wooden chopping board ONLINE IN INDIA
Cat Toys-With-Feathers Enjoy hours playing with your cat in a super fun way. Bright feather attract cats attention easily. Buy Online
ReplyDeletebuy cat toys ONLINE IN INDIA
Sales with QuickBooks Desktop and Online it will automate your bigcommerce quickbooks orders with inventory, shipping and accounting.
ReplyDeletePearl Shell LED Lamps
ReplyDeleteThe Alto diffuser uses ultrasonic waves to instantly evaporate water, creating a cool, dry aromatic mist Best mosaic Diffuser
ReplyDeleteGood Content! Thanks for sharing Keep it up Top 10 Ayurvedic Herbal PCD Companies in India
ReplyDelete
ReplyDeleteReally Nice Information It's Very Helpful Thanks for sharing such an informative post! Ayurvedic PCD Pharma Franchise in Chandigarh